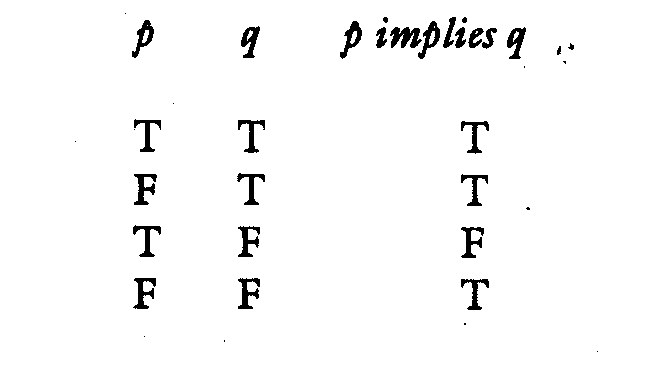
Compounding propositions
The preceding inferences were not called "syllogisms" because they involve only one premise, and "syllogism" is the Greek word for "a combined statement."
A syllogism is an inference with two premises.
As long as I have defined this, here are a couple more terms:
An enthymeme is a syllogism with one proposition not explicitly stated.
Enthymemes are often the way we reason in ordinary language, because the statements that are left out are so obvious that it insults the intelligence of the hearer to state them. In the informal use of logic, we also tend to put the conclusion first (as I am doing in this sentence), because we want to let the hearer know right away what we are driving at, and then give him the evidence for it. So you would say, "John is going to die, because every human being dies," rather than, "John is a human being, and every human being is something that will die, and so John is something that will die." You don't need to say, "John is a human being," because your hearer knows what you are referring to (not to some dog named "John"). Enthymemes can also leave out the conclusion, as obvious. You might say, referring to John's propensity for living dangerously, "Well, he's human, after all, and all of us have to die sometime." It would be insulting to your listener if you then said, "and so he has to die sometime too."
A sorites is a chaining of several syllogisms or enthymemes.
You might give this hypothetical sorites to someone, for instance: "If you try drugs for fun, then you might start doing drugs, and if you do drugs, then you're going to become an addict, and if you're an addict, you've got nothing to live for but drugs." In the informal use of logic, this would usually be followed by "Then why try drugs for fun?" which points first of all to the omitted conclusion, "If you try drugs for fun, you're going to have nothing to live for but drugs," and the following evaluative inference, "If you don't want to have nothing to live for but drugs, then don't try drugs for fun."
Now then, what are the ways we can combine two propositions so that we can generate a conclusion from their parts?
Let me first state a general rule that can be helpful, now that we are not at the moment getting inside a proposition and looking at its parts:
Rule: For purposes of combining whole propositions, a statement in any form is taken as a proposition.
That is, there isn't any special logical form for statements as components of compound propositions. This will not be true for the categorical syllogism, because it is precisely the way of compounding propositions because of the characteristics of the subjects and predicates of the combined propositions. But other types of syllogisms don't have to worry about how the components look.
Let me also make a couple of definitions to make what is going on in logic a little clearer.
The inferential mode of reasoning affirms the compound and affirms or denies one of its components, and concludes to the affirmation or denial of the other.
The refutational mode of reasoning affirms or denies each of the components and concludes to the affirmation or denial of the compound.
There may, of course, be more than two components in the compound proposition. "Either you're asleep or you're thinking of something else or you're stupid" is a perfectly legitimate compound proposition, for instance. In these cases, the rules for the compound with two components apply mutatis mutandis, and so I'm not going to discuss them further.
The reason why I called the second mode of reasoning "refutational" is that, as we will see, the inference from the components to the compound is only valid in proving that the compound is false, because the alleged connection between the components is not what the compound says it is. To understand this, we have to be clear about what the criteria are for a valid inference.
We need a couple of other terms:
An inference is sound when the premises are factually true statements, and they generate a conclusion which cannot be factually false. Otherwise, the inference is unsound, even if the conclusion happens to be true.
This is what we ordinarily mean by the "validity" of an inference, because we see no reason for a person giving premises which he doesn't think are true (i.e. they may be negative statements, but he considers them true, or why say them?). But the validity is something more hypothetical.
An inference is valid when, if the premises are true, the conclusion cannot not be false.
So for the logic to be valid, the premises don't have to be true, but when they're not, if they were, the conclusion would be true.
Criterion for a valid inference (contemporary): An inference is valid if when stated as a conditional proposition, it is true for all truth-values of the components.
This is another way of saying that in contemporary logic, the inference is valid its expression is a tautology. By "tautology" here is not meant simply "the same term is repeated," which is what we ordinarily mean by "tautology," such as "a blue bird is blue," or by its definition, such as "a valid inference is a potentially sound inference," but also such statements as "George Blair is not anything but George Blair." That is, any statement that fits the Principle of Identity we discussed in the Chapter 8 of Section 1 of the First Part 1.1.8 is what we ordinarily mean by a tautology (it says the same thing); but tautologies also apply to statements which fit the Principle of Contradiction (it amounts to the same thing).
Now contemporary logic talks about two kinds of fallacies, which mean that, in their system, the definition of soundness I have given above is not accurate. Contemporary logic's definition of soundness is "If the premises are true, the conclusion cannot be false." But "true" in contemporary logic does not mean exactly the same thing as what I mean by a "factually true statement."
The two kinds of fallacies can clear up what I am talking about. A formal fallacy in contemporary logic occurs either with a false premise or a violation of a logical rule. An informal fallacy would be using a word in "two different senses" (taking the same word as the same term, in my terminology, when in fact it is two different terms); or by concluding to something that was irrelevant to the premises--something that you could only discover by looking at the sense of what you were saying rather than the form as defined in contemporary logic.
Thus, for instance, to argue from the fact that George Bush is in the White house and the other fact that my feet hurt to "George Bush is in the White House and my feet hurt" is a sound argument in contemporary logic, because, given the truth of the premises, the conclusion can't be false.
But a person could say, "But Bush's presidency has nothing whatever to do with the state of your feet," meaning not that either of the two statements was false, but that the fact that each is true does not mean that you can conjoin them. Hence, the person would contend, it is false to join them into a single statement as if together the expressed a fact, when they in fact express two distinct facts.
In that sense, the premises can be true and the conclusion false. "But that isn't what we mean by 'false,'" the logician would say, "because 'and' as we use it does not say that both statements together form a statement of a fact, but merely that each expresses a fact. And, of course if each expresses a fact, it is sound to say that each expresses a fact (that is, it is a fact that each expresses a fact)." So the inference is sound.
Now what I am going to try to show in what follows is that in each case, if you take the meaning of the connective to be solely its logical function, then there is no occasion for anyone ever to utter as a statement of fact the proposition using the connective in this way. So factually, the inference is not sound.
And what I will conclude from this is that, even if logic as defined in contemporary terms is internally consistent, it has no application to statements of fact, because as statements of fact, its compound propositions (including the statements of its inferences) are "statements" that no one could have any reason for uttering in the sense contemporary logic intends them.
Let me here define what I mean by the logical function and the meaning of a connective:
The logical function of a connective combining statements (or propositions) is the indication of what is to be done with the statements connected.
The meaning of a connective is how the facts stated by the statements are interrelated.
For various reasons, some logicians who still hold that logic deals with the world "out there," like Bertrand Russell, for instance, have problems with "connected facts." But since, if you refer back to Chapter 6 of Section 5 of the first part 1.5.6(not to mention what leads up to it), for me a fact is a connection among objects (spelled out in terms of knowledge a little more in Section 3 of the third part), then I am not going to bother with trying to establish that there can be "factual interrelations."
I gave one example of the difference logical function and meaning with "and," which I will discuss more at length below; but just to be clear about it, let me say that the logical function says that each component must be affirmed (i.e. accepted as stating a fact), and the meaning adds to this that the two are somehow connected. To take another example, the statement, "If Chicago is in Illinois, then I am getting gray" illustrates the connective called the "implication." You are obviously bright enough to see pretty clearly how "if...then..." functions logically as a connective; but the reason why the statement sounds strange is of course that beyond this logical function, the connective also means "the second statement's being a fact depends in some way on the fact expressed first." Clearly, there is no dependence in the example.
My position is that the logical function of a connective is not divorced from its meaning, but included within it, so that if the logical function is violated, the connective is wrongly used (is false). But since the meaning goes beyond mere logical function, then the connective can be false and still used properly in its logical function.
Further, I contend that the logical function is derived from the meaning (i.e. depends on it) and is not just an adjunct to it;(1) that is, it is because facts have certain interrelations that statements have certain connections and not others, and you can't just stick in any connective you want at any given time and still hope to be describing the real world. For instance, the implication in statements occurs because effects really depend on causes for their existence, and we know this. That effects really depend on causes is the whole point of the first part of this book from Section 2 on; that we know this is the burden of Section 5 of that part and Section 3 of the third part. If there were not a connective such as "if...then...," we would have to invent one.
So what is at the base of my problem with contemporary logic is its epistemological stance that says that you can refer to the real world without taking into account the meaning of the connectives--or even worse, that the language is simply self-contained, referring to nothing outside itself, in which case to use it to critique the logic of what anyone else says is like criticizing a statement in French which happens to use words that look like English on the grounds that it doesn't make sense in English.
Of course, by that token, I would not be "allowed" to criticize what is said in contemporary logic because it doesn't make sense in my logical system. But that's only forbidden for a person who buys into the idea that a system can't apply outside itself, and I simply deny this for the same reason that I deny relativism, as I said in Section 1 of the first part. For a person within a self-contained system to issue a "rule" that criticism of his system from outside is invalid or illegitimate obviously contradicts the self-containedness he demands for his system (because he's criticizing some system outside his).
My contention is that there is a logic of statements, which may or may not be very complex and only approached by any known system of formal logic; but formal logic is an attempt to discover and formulate this logic. Hence some logics are better than others because they more accurately express more of how we in fact reason when we connect the expressions of our acts of understanding to generate what we realize are new relationships between objects from old ones.
If someone disagrees with this and
Should say,"That is not what I meant at all.
That is not it, at all."
my answer will be, I dare to eat a peach. Let her go her way, like the skeptics and the relativists of Section 1 of the first part. "And turning to [the reader] he said, 'Do you want to go away too?'"
This is not to say that I find contemporary logic inapplicable. As I said, the logical function of connectives is contained within their meaning; and so insofar as the connections between what is said depend on the logical function of the connectives, that version of logic will apply to it, and since anything connected depends at least on the logical function of the connective, then what violates contemporary logic (what is invalid in it) will be invalid for statements also; but there will be things that are allowed in contemporary logic that are fallacies in statement logic. Hence, contemporary logic can be safely used for refutational purposes only.
Because contemporary logic doesn't really tell you what to do with statements, I will give rules on the permitted and forbidden logical operations based on the meaning and function of the connectives in question. This is very close to Aristotelian logic.
Now then, contemporary logic's criterion for validity above needs some explaining, and in order to do so, I have to give you the truth table of the conditional proposition with its components. I will discuss the conditional proposition later; but for now, its truth table will allow me both to illustrate what a truth table is and show how it works.
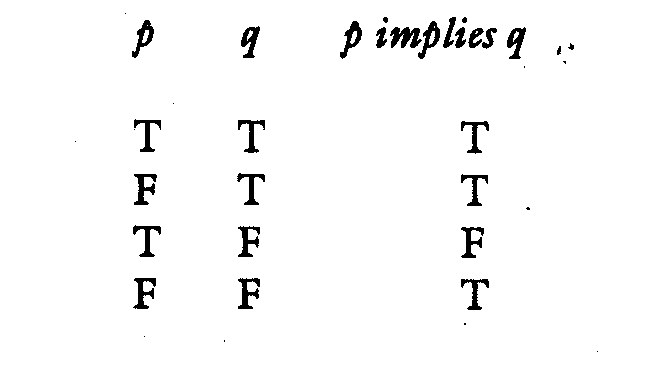
The first thing to note is that contemporary logic uses the letters "p" and following to indicate whole propositions in any form; and since we're not now interested in subjects and predicates, as I said, we can do this also. One convention here is that if the same letter appears twice, it stands for the same proposition both times. So "p" means "any old proposition," and "q" means any other proposition you please."
I am not, however, going to use contemporary logic's dots, V's, slashes, and horseshoes and so on that symbolize the connectives, because they make the whole thing terribly confusing to look at; and in a matter like this, unnecessary confusion is something you want to avoid if at all possible. So I will, as above, use the names of the connectives.
Now if you look at the T's and the F's in the first two columns, you will see that they exhaust all the possible combinations of affirmation and denial there are with two propositions. If there were three, there would be eight lines in the truth table; but as I said, we are only interested in the basic ideas, so we will stick with two propositions. The T's and F's in the third column are what the compound proposition turns out to be based on the logical function of the connective and the T's and F's on the corresponding line of the components' columns.(2) Thus, the first line says that when "p" and "q" are both true, the compound proposition "p implies q" is also true. For instance, the compound "If dogs are mammals, then dogs are animals" is true, given that both "dogs are mammals" is true and "dogs are animals" is true.
Don't confuse reading a line of the truth table with an inference, however; the truth table is just what you might call the "logical sense" of the compound proposition: a kind of "truth-definition" of it; it defines its truth-value based on the logical function of the connective, though not its meaning. This obviously has to be the case, since logic defines the meaning of the connective to be nothing but its logical function. We will see more of this distinction as time goes on.
But to return to the truth table of the conditional proposition, the inference above about Chicago would be expressed like this, with "Chicago is in Illinois" being "p" and "I am getting gray" "q."
[(p implies q) and p] implies q
The difference between the inference and this proposition is that "p" as an affirmative proposition is not the affirmation of "p," but simply a "proposal of 'p,'" one that is "proposed for the sake of argument." But it can be in reality false (and can be known to be false. That's what the truth tables are for). Similarly, a negative proposition is not a denial, because it is "proposed as" true and can be denied. Since an inference proceeds by way of affirmations and denials, this is simply the expression of an inference, which can be false in the various ways in which statements can be false, as we saw in Chapter 5 of Section 3 of the third part 3.3.5.
But a statement such as this expresses a valid inference (in contemporary logic) when as a complete statement, it is true all the time, no matter whether the component statements are true or false in themselves. That is, when the connective expressing the main verb (in this case, the "implies" on the right-hand side) is true all the time, no matter what p and q are themselves, then the inference is valid. This is what contemporary logic means by "a tautology."
The way you establish the validity of the inference is this:
First, knowing the truth table for "p implies q," you substitute the last column of that truth table for our the column that represents the parentheses, and at this stage we have
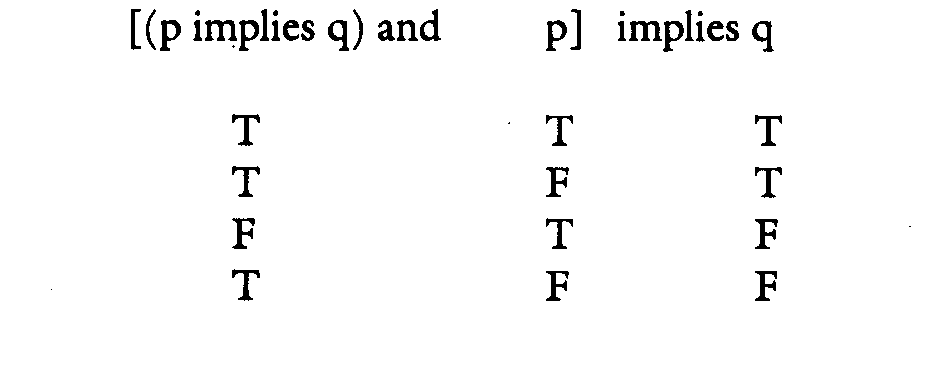
Now we have to look at the truth table for "p and q" (given below under the discussion of "and") to get the next stage; and that gives us (ignore the Ts and Fs in the square brackets for the moment):
Note that you can't read this table from left to right. You have to read first what has no parentheses or brackets around it, then what has parentheses, and lastly what has square brackets, then what is in braces.
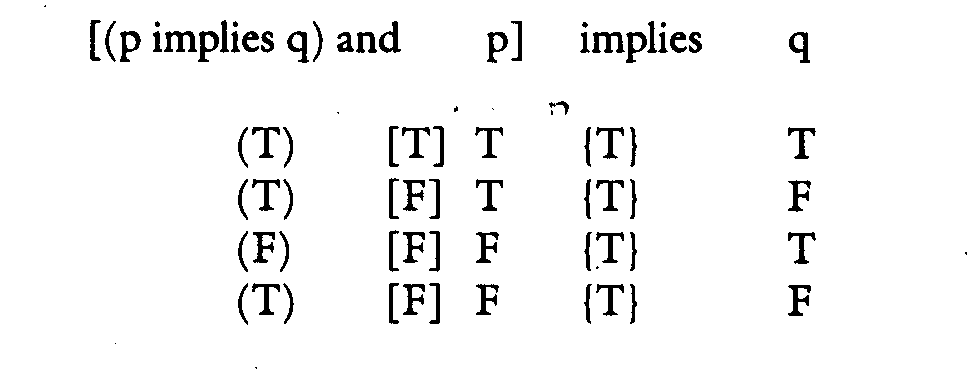
since "and" is only true when both components are true. Now we're ready for the last stage, expressed by the Ts and Fs in the square brackets. The column under "and" now is our new "p" and by the truth table for "p implies q" we see that the column for the last "implies" (the letters in square brackets) is all Ts, since it is T when the "p" is true and the "q" is true, and T when "p" is false no matter what "q" is.
Therefore, that inference is, as I said above, a tautology, or is valid, according to the contemporary criterion of validity.
With that out of the way, then, let us go to the first of our connectives, which is called a conjunction, of propositions, and simply asserts the fact that the propositions are connected:(3)
The logical function of "and" is that each of the component propositions is to be affirmed.
The meaning of "and" is that the two facts affirmed are connected somehow; but it does not specify what the connection is.
In the logic of statements, this is trivial. It is obvious from the logical function that if the compound proposition with "and" is to be affirmed (and why would you state it as a fact if you weren't affirming it?), then the only thing you can do is affirm each part. You can't deny either one, and the affirmation of one doesn't imply the affirmation of the other (the affirmation of the compound simply affirms both already).
The reason is that you can't affirm it unless you already know the truth of both parts, and so you would already explicitly know the "conclusion" before you drew it. So it isn't reasoning to say, "John is tall and John is strong; and John is tall; therefore, John is strong." The second "premise" is a waste of time, and the conclusion doesn't follow, because it was already stated in the compound proposition itself. And if you say, "John is tall and John is strong and John is not tall," you've already contradicted yourself explicitly.
In contemporary logic, this is how the truth table for "and" looks:

Now as I said with the conditional proposition above, this is just an assigning of truth values to "p and q" based on the logical function of the connective, and it is not an inference.
You can, however, make inferences based on it, even though when you see them translated back from symbols into sentences, they look silly. We saw one of them above, ("John is tall and John is strong, and John is tall implies John is strong.") which had the form [(p and q) and p] implies q. When all you see is the letters, this looks like an inference.
The truth table check on the proposition looks like what is below. Here, to save space, I have introduced a convention. Again, what is not enclosed in any kind of bracket is the initial stage of "p" and "q"; the result of the second stage is in parentheses; the result of the third in square brackets, and that of the fourth in braces (if there were more steps, they would be in double parentheses, double brackets, and so on).
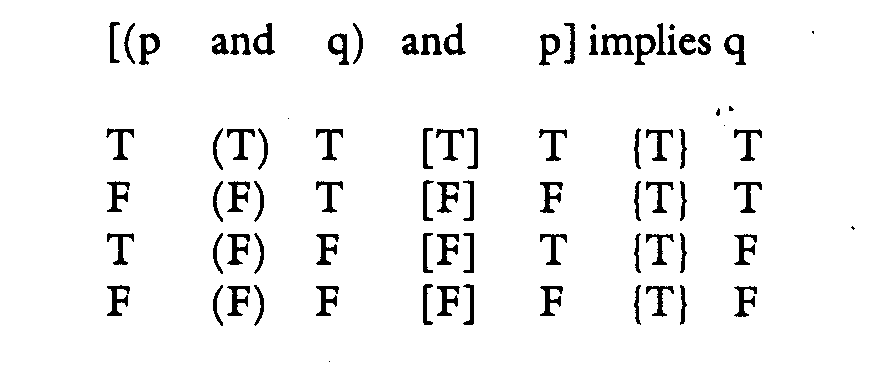
Since again the last step is all T's, the inference is once again valid. But as I said, no one would ever have any occasion to perform such an "inference."
If, however, we try to reason the other way, from the components to the compound, this is what we get, indicating the first compound by what is in the parentheses, and the final step by what is in the brackets:
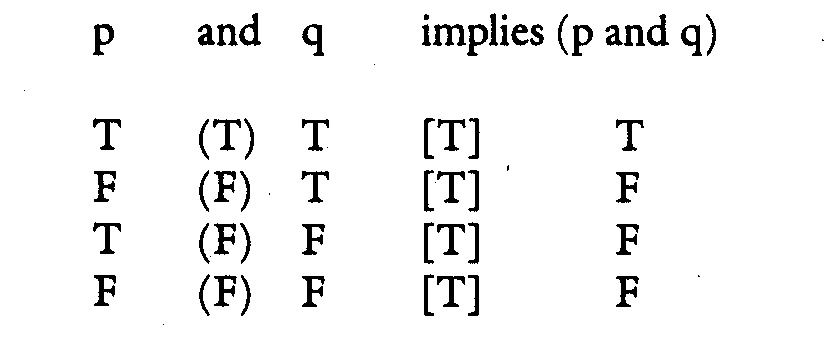
And here we run into the heart of my difficulty. For instance, why is the statement, "George Bush is in the White House and my feet hurt" funny? Because it connects two statements as if the facts were connected; and the humorist expects people to recognize that the facts are not in fact connected.
First note, however, that that's not quite what is being said in the conditional proposition above. That proposition actually says "If (George Bush is in the White House) and (my feet hurt), then George Bush is in the White House and my feet hurt." Well of course. But in making this into one sentence, you have to make the conjunction in the antecedent (the "if" clause), from which the consequent (the "then" clause) trivially follows. In other words, you have turned the inference into the form "p implies p."
But that isn't what the statements say. It is invalid to argue from a true statement and any other true statement to a conjunction of the two statements, because they might be conjoined or they might be totally unconnected. Putting the inference into a conditional proposition in contemporary logic can't spot that fallacy--and, indeed in contemporary formal logic, it isn't a fallacy, and the argument is sound, which means that the conclusion is true. Of course, it's true that any two true statements always can be conjoined (if under no other guise than that they're both examples of true statements); but the conjunction may or may not express and actual connection of some sort among the facts, or the statement about the President wouldn't be funny. Consequently, it does not follow in the logic of statements that the conjunction must be true when both of the components are true.
Contemporary logic's "and" is a weak "and," which does not say that both components (together) express something that is true, but merely that each is true. That is, it does not say that the two propositions are connected.
The question I raised above now arises of whether there could ever be a reason for using the connective in the sense defined by contemporary logic.
I don't see how there could be, because of the fact that the two propositions are connected into one sentence (one compound proposition); and it is bound to be misleading to connect two things which explicitly are not to be taken as connected.
Now you can say if you want, "When I connect things, they might be connected and they might not, and so you aren't to understand them as connected." My answer would be, "If you don't want me to understand them as connected, don't connect them." Instead of saying "p and q" as one proposition, state two distinct propositions: "p" period. "q" period. That leaves it open as to whether the two are connected or not, since it precisely says nothing about it. It's certainly possible to do this rather than redefine "and" to be something that no one else would ever use.
In other words, the very act of connecting the two propositions into one contradicts the "definition" in contemporary logic of the connective as something-that-does-not-express-a-connection. You can say, of course, that no facts are connected, and so "and" can't mean anything but the convenience of getting the propositions in convenient shape to be worked on; but that's the epistemological stance I think is simply silly, or statements like the one about the President wouldn't be funny. Such statements recognize that some statements express connections between the facts represented and some statements don't. Hence, "and" means something.
Logicians preen themselves on being unambiguous and on saying no more and just precisely what they mean. But I don't personally see how you can avoid ambiguity when you connect things that may not be connected. Better to reserve "and" for propositions that express what is somehow connected; then you leave no ambiguity in what you are doing. The logicians would object that they want all the propositions in an inference to be expressed as one single proposition. Very well, then the ambiguity can't be escaped; but don't claim that you're being unambiguous.
So much for my first argument against the validity of contemporary logic as a system. If we now look at the next connection, said to be a a form of "or," but which I call "is incompatible with" in its clearest formulation, my problem with contemporary logic will be a little clearer.
The logical function of "is incompatible with" is that at least one of the components must be denied.
The meaning of "is incompatible with" is that the facts stated in the components are incompatible with one another.
This connective is not logically trivial, because all you know by affirming the compound is that one or the other, and possibly both of the components must be denied (is false), but you don't know which one. And as a statement it is not trivial either, because what you are asserting by the compound is the fact of incompatibility between the components, not necessarily any knowledge of the factuality of either of them.
Generally in common speech, this connection is stated negatively; either as an impossibility, as in "you can't have your cake and eat it," or more often of the form "not p when q" as in "The cat is not outside when it is raining." Or possibly the statements are given as gerundives connected with "is incompatible with" as in "The cat's being outside is incompatible with its being rainy." Note that the second proposition looks as if its first part is a denial; but the "when" shows that the denial belongs to the whole statement. It means "It is not the case that the cat is outside when it is raining," or "It is not, as a general rule, (the force of the "when," as we will see below) simultaneously true that the cat is outside and it is raining."
Here what I am going to do is say what I think is wrong with contemporary logic's approach to the proposition, and then afterwards list the valid inferences that can be made from it. Once again, I think that contemporary logic's ignoring of the meaning of the connective allows it to make "valid" inferences that are fallacies when taken as statements. Let us look at the truth table:
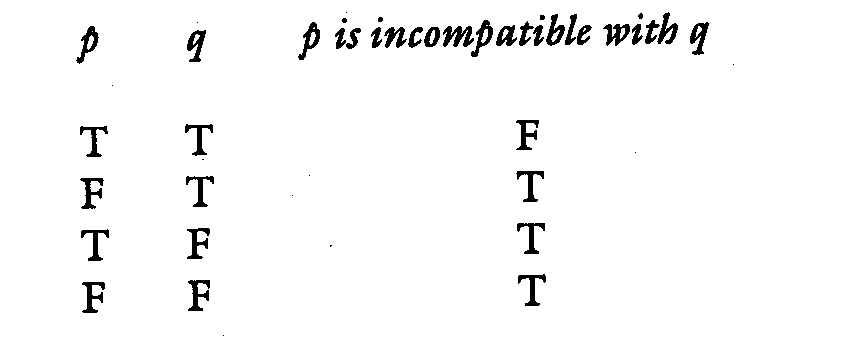
which is just the opposite of "and," you'll notice; and in fact, it is the logical equivalent of "not (p and q)." And here is the problem. The statement, as I will try to show, is not merely the denial of a conjunction.
Observe that, if you affirm both components, you necessarily have to deny the connection and so there is a legitimate inference this way. For example, if you say, "The cat is not outside when it's raining," you can prove the connection inappropriate by showing an instance when the cat is outside and it is raining (i.e. by affirming both). So this inference works in both contemporary and statement logic.
But the difficulty with contemporary logic, as I said, is not in its refutational use, but in its use in an affirmative sense; and the reason is below:
The meaning of "is incompatible with" in contemporary logic is a weak "is incompatible with," which simply denies that both components are true, but says nothing about whether they are incompatible with each other, but simply that one or the other or each is false.
Now it might seem that I've loaded the dice here, because what I call "is incompatible with," contemporary logic (when it uses this connective at all, which is very seldom) simply calls it "not both." But what I am going to try to show is that to take the compound in the sense of "The two don't happen simultaneously to be true" produces a statement that there would be no reason for making.(4)
To begin, then, the meaning of the proposition as contemporary logic would have it could not be expressed as "The cat is not in the house when it's raining", because the "when"makes it a general statement (i.e. of what is always the case), and so rules out the statement as merely a simple statement of what is going on now. As a simple statement of what's going on at present (a negative conjunction), it would be stated, "It isn't simultaneously true at the moment that the cat is outside and it's raining." Here, all you would be intending to state is just that the two happen not to be the case.
But could you make a statement "It is not simultaneously true that p and q" as a simple statement of fact, totally unconnected with any general rule? It would be difficult to imagine an occasion for it. First of all, in this case, how could you know whether it was true as a whole or not without knowing anything of the truth or falseness of at least one of the components? That is, how could you possibly assert as now the case that it's not simultaneously true that the cat is outside and it's raining without knowing whether either of these were true or not? So you can't make it without knowing something about the components.
Secondly, if you know one of them is true, you still can't assert that the conjunction is false (even contemporary logic says this), because, for all you know, the other one might be true, making your proposition false. That is, if you know that the cat is outside and that's all, you don't know that its false that the cat is outside and it's raining--unless, of course you knew the general rule that the two are incompatible. But we're not talking now about incompatibility, but simple statements of fact.
Thirdly, if you already knew that one component was false, why would you conjoin the opposite of this false statement with any other proposition? That is, if all you know is that it's not raining, why would you then say, "It isn't simultaneously true that it's raining and Lincoln is in the White House.")? Here again we have the problem of connecting two propositions into a single compound proposition with absolutely reason to connect them. The only "grounds" you could give is that you happen to know that the opposite of one of the components is true; but those "grounds" are exactly as good for connecting, "It's not simultaneously true at the moment that there's life on Mars and the temperature in Miami is ninety degrees."
Fourthly, if you know that one is true and the other false, you would be giving misleading information. The reason is that if you're trying to convey to someone what is the case, and you know that the cat is outside and it's not raining, then to say "It's not simultaneously true that the cat's outside and it's raining," conveys the information that both might be false, which is impossible as a statement of the present situation, because one is true.
Finally, if you know that both are false, and you want to tell someone what the present state of affairs is, you would say, "The cat is not outside and it's not raining," denying each of them, not denying the conjunction, because that also conveys that one of them might be true, when in fact, neither of them can be true because they're both false.
So I submit, therefore, that it is unreasonable to make an "is incompatible with" statement of fact as a mere statement of what is at present the case. If you have no information at all, then you can't make the statement; if you know the truth of one, you can't do it either, because it doesn't follow; if you know the falseness of one, then the statement you make has no connection with the information you have; if you know the falseness of one and the truth of the other, you're conveying the false information that both might be false; and if you know that both are false, you're conveying the false information that one might be true.
This is not to say that the statement might not sometimes be true, as in the case of knowing that one is false and the other true; but in that case it is unjustified, which means it is made capriciously. It is also possible that the context could be peculiar enough so that the misleading information in the last two instances would be removed (as, for instance if you actually gave the information you knew first); but in that case, it would be superfluous, because you would previously have given more information than you give by the statement.
Let me just illustrate this last case. You could say, "The cat is not outside and it's raining out, and it's not simultaneously true at the moment that the cat is outside and it's raining out." But why would you ever say a thing like that? Even if you said, "The cat is not outside and it's raining out, and so (i.e. implies) it's false at the moment that the cat is outside and it's raining out," that's just as bad. In neither of these two cases have you conveyed any more information by the second part of the statement. Everyone would recognize that what you said was true, but making the statement would be completely redundant. So either such a statement is redundantly repetitious pleonastic superfluity, or it is misleading.
A word on ambiguity. Logicians, as I mentioned, like to think that their meaning of the connectives avoids ambiguity. But the "is incompatible with" proposition is precisely ambiguous. That is, it leaves open three possibilities: "p" is false, "q" is false, and both are false, but does not distinguish among them. Now to leave open three interpretations of the proposition without picking out one is to leave the proposition ambiguous in its truth value. Granted, the connective is precise in its logical function, because these are the possibilities and there are no more and no fewer; but it isn't speaking precisely (or unambiguously for that matter) to confuse precision with unambiguity.
So much for that. Now could the "is incompatible with" (in the weak sense of "not in fact both") statement be made as a statement of what has frequently been the case, without implying any incompatibility between the two statements and without grossly misleading your hearer? (Contemporary logicians tend to say, remember, that their way of speaking is the way we "ought" to speak to make ourselves clear.)
That is, can "The cat is not outside when it's raining" convey, "I've never so far seen the cat outside when it's been raining (but it might happen tomorrow)." In that case, the use of the present tense is what is misleading. If all you are trying to convey is something that so far has invariably happened and not that there are grounds for predicting anything from this, then the present perfect tense must be used. The present tense is used only for present states of affairs or general statements that occur irrespective of time (and so would also occur, presumably, in the future).
For example, the simple denial as having happened invariably but without predictive implications might be spoken by, say, the President's wife: "I've never been in this room when George Bush has been in it." Clearly, if she said this, she would not be intending to convey any hint of what might happen five minutes from now. But if she said, "I'm not in this room when George Bush is in it," this would be a general statement, and so it would be taken as having a predictive value also, as implying that for some reason she is not permitted in the room when the President is there (or that she refuses to be in it when he's there). So to say, that "is incompatible with" means that "it is not the case that p and q" cannot be taken to mean, "It has so far not been the case that p and q."
Of course, if you want to adopt Hume's criterion of causality, then of course you could say that no general proposition (except a tautology) has any predictive force, and all are simply summations of what has been observed so far. But I fail to see how you could make such a general proposition, because it's a general proposition which is not a tautology. In that case, if it is true, it would only apply to the ones you have seen so far, and would have no bearing on any other one. And again, your statement of it would be misleading, because all you meant to say was, "So far, I haven't run across any non-tautological general proposition that has any predictive force, but the next one might be one," like Mrs. Bush's past-tense statement above. But then why say no general statement allows you to know anything beyond what is observed? You certainly mislead people into thinking that this general statement applies beyond the ones you've seen.
So to say that the "is incompatible with" statement merely means that so far the two parts have not happened to be conjoined is to convey by the use of the present tense that they are incompatible, when you don't want to assert that.(5)
Hence, the only way you can be clear in what you are trying to say with an "is incompatible with" statement is that it asserts what you think is the fact of incompatibility between the two components. You are not asserting the grounds you have for this, but merely what you consider the fact. Hence, you may know that your cat hates to get wet, and so you say, "The cat is not outside when it's raining." All your hearer knows is that you are asserting that it is impossible for both components to be true--not that you are asserting that they are not both in fact true at the moment.
Where are we, then?
Conclusion 2: The weak "is incompatible with" statement of contemporary logic has for practical purposes no occasion to be made as a statement.
Let me, then, give the rules for the "is incompatible with" compound, given that it expresses the incompatibility of the components:
Rules for "is incompatible with"
Inferential mode:
1. If the compound and one of the components is affirmed it follows that the other must be denied.
2. If the compound and one of the components is denied, no conclusion follows.
Refutational mode
3. If both of the components are affirmed, the compound must be denied. This refutes the connection.
4. If one of the components is denied, nothing follows with respect to the compound.
The next connective is the contrary of "is incompatible with," and is sometimes called the "inclusive or"; it is usually stated "and/or" in informal speech; essentially, it is "not neither."
The logical function of "and/or" is that at least one of the component propositions must be affirmed.
The meaning of "and/or" is that the possibilities referred to are connected in such a way that one of them is in fact realized, though which is realized is not expressed by the statement.
This will obviously take a little clarifying. First, in ordinary use of this connective, the compound statement can also be stated "One or the other or both," to distinguish it from the disjunction, which we will see after this. The word "or" in English is ambiguous, since it can mean "one or the other" or "one or the other or both," and so clear speakers and writers use "Either...or" and "and/or" (or "(Either)...or...or both") when there is a danger that the context will not distinguish the two.
For instance, a person might say, in reference to some scandal "Either there's something wrong with the corporate structure, or management is corrupt, or both," or "that cat is clever or lucky or both."
What this connection actually asserts as a fact is the necessity of at least one of the components, usually because they are assumed to be an exhaustive list of the explanations of some affected object (which, if you will recall from Chapter 1 of Section 2 of the first part 1.2.1, is a contradiction by itself, but which as concrete can have a complicated causer). Explanations do not necessarily exclude each other (as, for example, the scandal in the corporation might be partly due to a faulty corporate structure and partly to corrupt management); but there has to be at least one; and if you list them all then they can't all be eliminated.
The proposition is refuted by denying both components, because of the fact that the components listed (which may be more than two, of course) is asserted to be exhaustive. But like the compounds we have seen already, it is not confirmed by affirming one of the components, or even both of them, because there might be another item to the list not taken into account. For instance, the clever and/or lucky cat above, in order to escape the dangers that occasioned the remark, might be being watched over by its owner, in which case it might be true that it's neither clever not lucky, but just loved. Or, of course, it could be all three. So, even though the cat's being clever is consistent with "That cat is either clever or lucky or both," it doesn't prove that the statement has to be true.
I suppose I should point out here that in contemporary logic, there is a valid inference from "p" to "p and/or q," which suffers from the informal flaw that something appears in the conclusion which was not in the premise. Formally speaking, the argument "The cat is clever. Therefore, the cat is either clever or lucky or both" is sound if the cat is clever (because if it's clever, obviously it's clever, making the "and/or" proposition true by default). But the compound proposition as a compound is then irrelevant to the argument, and so even in contemporary logic, it doesn't belong there, but by the informal fallacy of irrelevance.
Here is the truth table for this compound:
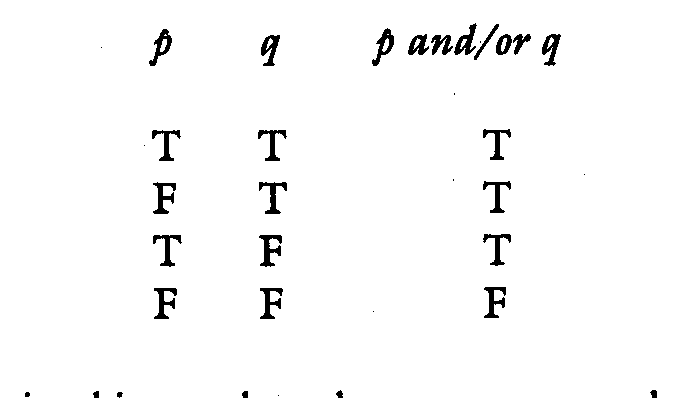
And once again, this says that what contemporary logic means by "and/or" is not and/or, but a denial that both are false, which can be a mere statement of fact. That is, if "p" is true, it is obviously false that both "p" and "q" are false; and that is what the "inference" above has to mean.
The "and/or" of contemporary logic is a weak "and/or" which simply means that one proposition is true, and says nothing about whether one has to be true or not.
We must again discuss whether we can ever sensibly make such an "and/or" as a statement of fact. Clearly, with no information about either component, it can't be asserted. If all that is known is that one component is false, it doesn't follow that the compound is true, because the other proposition could be false, making the compound possibly false. If all that is known is that one proposition is true, then this does not constitute sufficient grounds for connecting it with the other proposition, because any other proposition, true or false, would on these grounds fit just as well. Why would you, knowing that George Bush is President, convey information to someone by saying, "George Bush is President, and/or there is life on Mars"? It's true, but you have no reason for saying it. If you know that one is true and the other false, you are misleading your hearer into thinking that both might be true when they can't be--as a mere statement of fact, because what is in fact false can't be true if it's false. And similarly, if you know that both are true you would be conveying the false information that one might be false when it can't be.
This also is subject to the same sort of qualifications as with the "is incompatible with" statement as a mere statement of fact. It could be said, and it would not be false, but it would be either misleading or capricious to say it. And with that, we can draw the following conclusion.
Conclusion 3: There is for practical purposes no occasion where contemporary logic's "and/or" could be uttered as a mere statement of fact.
But if "and/or" means that at least one component must be true, then it would be self-contradictory if the list of possibilities wasn't exhaustive, because you would then be asserting that one must be true when both could be in fact false.
Here again we have a logical aspect of statements that is not covered by contemporary logic, which does not recognize "That's not all the alternatives" as a denial--as in fact it is in every case of the use of the "and/or" proposition. But of course, that refutation doesn't involve anything within logic, which is what contemporary logic wanted to avoid. But in that case, what it should have said is that no conclusion can be drawn from knowing the truth of one component, not construct the logical system in such a way that the conclusion is valid by making up this "weak" sense of "and/or" which never has been used and never will be. Why not rule out the "formally valid but not necessarily always the case" with its ambiguous use of "true," by stating a rule that the statement is meaningless as a mere statement of fact and is to be used when there is an exhaustive list of possibilities? Then the logical function would be allowed to do its work properly.
And this is precisely what the rules below do. Recognizing that "and/or" as used as a statement implies the necessity of one component's being true, here are the logical things you can do with it:
Rules for "and/or"
Inferential mode:
1. If the compound and one of the components are affirmed, no conclusion follows.
2. If the compound is affirmed and one of the components is denied, it follows that the other must be affirmed.
Refutational mode:
3. If one or both components are affirmed, nothing follows with respect to the compound.
4. If both of the components are denied, the compound must be denied. This refutes the connection.
The next connection, "either/or," is given the name "the exclusive 'or'" in contemporary logic; and in Aristotelian logic, the inference made from it is called the "disjunctive syllogism," because it is a more common way of reasoning than either of the two we have discussed. Actually, the commonest fallacy dealing with both "is incompatible with" and "and/or" is that (since they can be stated using simply "or") they are apt to be confused with this one (while in fact, "either/or" is another way of saying "not both and not neither").
The logical function of "either/or" is that one of the components must be affirmed and the other one denied.
The meaning of "either/or" is that the two facts referred to contradict each other.
Here is the truth table for the proposition in contemporary logic:

Once again (and I will again leave you to take my word for it or do it out yourself) we have a case of the fact that you can conclude to a denial of the compound (and so a refutation of the connection) by either affirming both or denying both of the components.
But you can't confirm the fact of the compound by affirming one component and denying the other (because the actual fact might be either a not-both or a not-neither compound, both of which are compatible with one component's being true and the other false). Thus, for example, "Either you're in New York or you're in Chicago" can't be established by saying that you are in fact in New York and not in Chicago--because clearly the proposition is actually an "is incompatible with" proposition that's disguised by the use of the wrong connective (i.e. as stated, it would be refuted if you were in Cincinnati).
Note, however, that doing out the truth table check will show you that the proposition "p and not q implies either p or q" is a valid inference in contemporary logic. Here there is not, as in "and/or," a rule of irrelevance to eliminate this fallacy. In contemporary logic, it is valid, and if the premises are true, sound.
Either/or as used in contemporary logic is a weak "either/or" which simply asserts that one component is true and the other false without saying anything about whether this has to be the case or not.
There is again something funny going on, which is masked in the example, because being in New York and Chicago are incompatible. But if we take two propositions that are compatible but don't have to be simultaneously the case, we can see how strange the meaning of the connective in contemporary logic is. It would be odd to say, "You are healthy and you are not six feet tall" implies that you are either healthy or six feet tall, because "you are either healthy or six feet tall" (the "exclusive" use of "or") seems to be saying that you can't be both. Well of course you can't be both if you're not in fact six feet tall; but to offer this is to use "can't" in two senses. One means "being healthy is in itself incompatible with being six feet tall," while the other means "both are not the case, and so at the moment they happen to be incompatible." But if you want to say simply "One and not the other" why not say that instead of saying "Either one or the other"? That is, why open up the ambiguity by using "Either/or" when "p and not q" would be clear?
Here again, logic is not being unambiguous. The "exclusive or" in contemporary logic does not exclude either "is incompatible with" or "and/or" in two out of the four cases in its truth table. Hence, the following proposition expresses a valid inference:
p and not q implies (p is incompatible with q) and (p and/or q) and (either p or q).
If we fill in the p's and q's, we get, "The fact that you're healthy and not six feet tall implies simultaneously that you're healthy when you're not six feet tall, you're healthy and/or six feet tall, and you're either healthy or six feet tall." That sounds really peculiar, but you can make sense out of it if you say, "If you're healthy and you're not six feet tall, then you're not both healthy and six feet tall, you're not neither healthy nor six feet tall, and you're one or the other."
But of course, when you put it this way, it is trivial as a statement. If you put it the way it was originally stated, then even ignoring the impression someone might get from the first conclusion that you're trying to say that you're healthy only when you're six feet tall (i.e. that your being healthy is incompatible with your being six feet tall), why would you say "you're healthy and/or six feet tall, and you're either healthy or six feet tall"?
That is, "and/or" includes the possibility of both, while "either/or" excludes that possibility. And here is where the two senses of "can't" mentioned above come in. In contemporary logic, "and/or" is true in this proposition because in itself it is possible for both to be true, but "either/or" is true, because as it happens they can't both be true because one is in fact false. And then there's the fact that "and" in logic doesn't mean "and."
So you have to be very, very careful if you're going to apply contemporary logic to statements. They don't mean what they seem to mean.
Warning: When contemporary logic talks about something being "impossible," this can mean simply that it is not the case.
This is the celebrated unambiguity of contemporary logic?
Further, as this example shows, to call "either/or" the exclusive "or" is to give the impression that it is incompatible with "is incompatible with" (in which both can be true) and also with "and/or," (which, after all, is called the "inclusive or"). But it isn't; it's inclusive of both of them in the sense in which the intersection of a set is inclusive of the two sets that intersect in it (i.e. it is the set that includes part of each of them).
And once again the problem is in the fact that contemporary logic does not recognize the additional information in the meaning of the connective. "Either/or" is in fact used only when the two propositions in question contradict each other, or only when you have grounds for saying that one has to be true and the other false, not merely when one happens to be true and the other happens to be false. If you say, "Well, it can be used simply as meaning "one and not the other," then I say that contemporary logic's goal to be clearer than ordinary speech has been violated. If you're stating it as a mere fact and not based on some internal contradiction, then you have to know which one is true and which one is false, and so why do you make the ambiguous statement, "One or the other of these is true and the other one is false" instead of telling what you know? Or why not use "and/or," if you want to leave open the possibility that both can be true?
I'll tell you this much. There are plenty of contemporary logicians who are not clear about the distinction I have been making, and who think that it's English that conveys inexact information and logic that always means exactly what it says. If it does, it certainly doesn't convey to the unsuspecting what it's saying.
Let's face it; in any rational system of logic, it is improper to use either/or when both can be true, even though one in fact happens to be true; that is "and/or," not "either/or," no matter how much you may be able to justify it using that etiolated sense of "can't." And the same goes for using "either/or" as in the New York and Chicago statement above, where the proper connective is "is incompatible with."
From this it follows that reasoning to "either/or" from "p and not q" ought to be forbidden. And that, in fact, is what traditional logic has done for millennia. If it is a convention to forbid it, then that convention is closer to the way statements are made (in Greek, Latin, English, Chinese, and Swahili) than contemporary logic's convention of taking "either/or" to mean no more than "one and not the other."
Then let me list the rules for how the disjunctive syllogism actually works:
Rules for the disjunctive syllogism
Inferential mode
1. If the compound and one of the components is affirmed, it follows that the other must be denied.
2. If the compound is affirmed and one of the components is denied, it follows that the other must be affirmed.
Refutational mode
3. If both of the components are affirmed, it it follows that the compound must be denied. This refutes the connection.
4. If both of the components are denied, it follows that the compound must be denied. This refutes the connection.
5. If one component is affirmed and the other denied, nothing follows with respect to the compound.
The final basic way logic combines propositions is the one we saw proleptically, called the "implication," or the "conditional proposition." or in traditional Aristotelian logic, the "hypothetical syllogism" (from hypo-thesis, a "putting under" or "supposition," because "q" "supposes" "p" "underneath" its intelligibility somehow, as an effect "supposes" its cause. It is stated either "if p then q" or "p implies q"; it is the general form of the inference, according to contemporary logicians, although it is not as they use it itself an inference because in order to make an inference you have to affirm or deny the p's and q's; but as the form of the inference, it's supposed to reflect the kind of thing you're doing when you make an inference.
Well it doesn't, as I think has been made clear. But before I discuss it further, let me state the function and meaning of the compound:
The logical function of "if then" is that an affirmation of the antecedent (the contents of the "if" clause) demands an affirmation of the consequent (the contents of the "then" clause), and a denial of the consequent demands a denial of the antecedent.
The meaning of "if then" is that the consequent depends somehow on the antecedent.
It is here that contemporary logic really takes flight into never-never land. Since contemporary logic wants to have nothing to do with things like question marks and wants its truth tables filled with either Ts or Fs, then this proposition elevates the non sequitur into a legitimate implication.
I already gave the truth table for this type of proposition when I introduced this section on compounding propositions, so I refer you back there if you want to look at it.
Now it is true that, since formal logic deals with the form under which statements go together, the contents of the statements don't enter into it. There was no problem with this in Aristotelian logic, because it always used the inferential mode of reasoning ("sophistical refutations" was an area that wasn't strictly formal); and in the inferential mode you always first affirm the compound and then argue to the components. Hence, if the compound is some non sequitur like, "If I schedule an outdoor party, then it rains," it doesn't matter; because, assuming that compound statement to be true, then you can make it rain by scheduling a party, or you can guarantee that there'll be no party by noticing that the day is sunny.
But in the real world, if you're going to argue from the truth of the components to the truth of the compound, then the meaning of the connective can't be ignored; because the truth of the compound implication as a factual statement depends on whether the consequent in fact depends on the antecedent. That is, what you would be saying with respect to the compound above is that scheduling a party and having it rain proves that scheduling a party implies having it rain, which of course is ridiculous. That's the first problem, and it's the same one as we had with other compounds as treated by contemporary logic.
The implication in contemporary logic's conditional proposition is a weak implication (called "material implication,") because all it means is that it is false that simultaneously the antecedent is true and the consequent false, and says nothing about whether the consequent follows from the antecedent.
There has been a firestorm about this particular deviation of contemporary logic from the way we use statements, because it is obvious that "implies" as a word means more than a denial of "p and not q."
I said that it is a valid inference in contemporary logic from "p and not q" to "p is incompatible with q, p and/or q, and either p or q." But now (and you can work this out on the truth tables if you want), it is a valid inference from "not p and q" to "p is incompatible with q, p and/or q, either p or q, and p implies q."
Come again? It's a valid inference from "not p and q" to "p implies q"? Knowing that the Cincinnati Reds are losing their game today and that it's raining out proves that if the Reds are winning, then it's raining? (Yes. It also proves, by the way, that if the Reds are winning, then it's not raining.)
I think you can see why this has caused something of a problem.
Warning: Even though material implication uses the word "implies," it is compatible with the absolute independence of the two components from one another.
The only requirement for saying that "p implies q" is that the combination of "p's" happening to be true and "q's" happening to be false is forbidden. Why? Because the inventors of this logic decreed that it is, not because of anything about "p" and "q," certainly, and not because the connective "implies" means this. Everyone who has ever struggled with contemporary logic has to spend a great deal of time erasing any meaning to "implies" that has anything to do with a sequence or a dependence or anything else; and of course, once they do this, they think they've finally "mastered" something very difficult, and they fight tooth and nail for how "powerful" material implication is and how much more "accurate" it is than the messy way we talk, and all the rest of it.
Now "formal implication" (that is, "implication" in the sane sense of the word, expressing dependence) also makes it impossible for "p" to be true and "q" false, so some of the invalid inferences in "formal implication" are also invalid in material implication, and all of the invalid inferences in material implication are also invalid in formal implication. But there certainly are valid inferences using material implication that are invalid by any rational standard of when something follows. For instance, let us try to unpack the inference above about the Reds, to see if head or tail can be made of it in any sense. First of all, I can eliminate some of the confusion by saying that the conclusion also follows from the mere fact of "p's" being false (you don't also have to know that "q" is true).(6)
So in this slightly easier form, what it says is "It's always true to say that if it's false that the Reds are winning, then it's true that if the Reds are winning, then it's raining."
But that's still a little difficult; let's take a simpler example: If I am here, then I am at home. Now when it's false that I am here, it is legitimate in contemporary logic to infer that if I am here I am at home--no matter where I actually happen to be. (To avoid quibbles, I mean by "here" a certain address I could give you.) Granted, it happens to be true that here is my home, so if I am here, I am at home. But it certainly doesn't follow that if I am in Chicago, then if I am here I am at home (that is, that my being in Chicago establishes where my home is).
Now then, the first thing to remember is that this is a negative statement in contemporary logic, not an affirmative one. So "If I am here, I am at home," is actually the statement, "'I am here and not at home' is false"; this is what is said to "be implied" by my not being here. Now what that says is not an implication, but another negative statement; so the whole thing becomes "'"I am not here" and "I am here and not at home is false" is false' is false." The last "is false" is the denial which is the basic "implication." The next-to last is because is the denial of the "q" part of the basic implication (it is, remember, not (p and not q). The third from last is the denial which forms the embedded "implication," and the "not at home" is of course the denial of the "q" in that embedded implication.
But two of these last three "is false's" cancel each other out, so simplifying, we get (putting, for clarity, the last "is false" first now), "It is false to say that "I am not here and I am here and not at home."
Well of course that's false, because it's false to say that I'm not here and I'm here, wherever my home is. So this proposition is going to be false because hidden in it is "not p and p," not because anything depends on anything else.
Warning: "Implications" which use material implication are really just negative propositions.
You know, I don't think much of a logical system that says it is "making an argument" when in fact it is making a denial. If this is what these people mean by "speaking precisely," and "saying exactly what you mean," I would hate to hear them speak imprecisely and say what they mean inexactly.
The justification for taking "p implies q" to mean "not (p and not q)" rather than "q depends on p," (which only implies "not (p and not q)") is that there are allegedly ambiguous uses of "p implies q" in ordinary speech, where sometimes causal dependence is meant, sometimes rule-following dependence (as in logic), sometimes mere sequential dependence (as in winter's implying spring to follow), and so on; and then there's the statement, "If you win this bet, I'll eat my hat," where something absurd is made to "depend on" what the speaker considers a false statement. Obviously, that can't be dependence, these people say; and so the "common core of meaning" is the negative proposition above.
But in the last case, that statement is a premise of an enthymeme, which the speaker thinks the hearer is too intelligent for the speaker to have to flesh it out. For the benefit of our logicians, let us do so. What is conveys to anyone with any sense is, "If you win this bet, I'll eat my hat, and I'm not going to eat my hat; and so it's impossible for you to win this bet." Knowing that a false consequent refutes the antecedent, a proposition which someone wants emphatically to deny is made to imply something known to be false. It is a rhetorical device, and the first proposition was not "proposed" as false, but as problematic until the false "conclusion" was stated. So it isn't that "anything follows from a false statement"; it is the perfectly legitimate reasoning that anything that implies a false statement has to be false. So that usage does not by any means mean that in ordinary discourse we ever use "implies" without the notion of some kind of dependence.
Now even if every case of "p implies q" makes "not (p and not q)" true, it is a far cry from that to say that "p implies q" means (or even "really means" or "ought to mean, if you want to be accurate") "not (p and not q)." This is about as intelligent as saying that since every human being can talk, then what is "really meant" by "human being" is "talker." Humans can do a lot besides talk.
Then why did the logicians get into that convoluted way of reasoning by turning the process into negative propositions that have negative propositions embedded inside them? The basic reason was that they didn't want to have compound propositions with anything but Ts and Fs in the truth tables, and in actual implications, you'd have to put a question mark in a couple of places.
But if you take this ploy, then to follow what is going on in the simplest inference then becomes an enormously tedious task involving negations of negative negations, trying to keep them straight as above.
Now of course, you don't have to follow an argument using contemporary logic. You can simply state it and then set up your computer to do the truth tables and wait until it spits out the truth table for the final result. Then you know that your conclusion is valid or not by the standards of contemporary logic; but of course, if it turns out to be valid, you still don't know whether it's only "formally" valid and not--shall we say?--existentially so without going back over it and trying to spot the "informal" fallacies.
Note that there is nothing that is invalid in contemporary logic that is not invalid in traditional Aristotelian logic, and so nothing is gained by using contemporary logic to spot fallacies. But there are conclusions that are valid in contemporary logic that are simply nonsense as statements of fact.
I will now consider that I have proved that contemporary logic is a waste of time; and this applies both to "propositional logic" (where you don't care what the proposition looks like but just combine whole propositions) and "predicate logic," (where you care about subjects and predicates), because the definite proposition in contemporary "predicate logic" has the form of the implication and so is infected with the disease of material implication.(7)
But why did logicians develop this system? It was partly to get out of a Hegelian idealism, whose logic, you will remember, was the logic of contradictions, and was also "metaphysics" in his sense of the term. That was the main incentive for purging logic of all Hegel stuffed into it.
But it was also true that the inventors of the system (particularly Boole) were mathematicians, and, like mathematicians, they wanted to develop a system of logic that was "closed and complete." A system is closed if all the conclusions from premises within the system are still inside the system, and it is complete if every operation on meaningful statements within the system results in a meaningful statement. Thus, addition is closed and complete on the set of the natural numbers, because any number added to any other number yields a natural number (natural numbers are {1,2,3,...}). Subtraction is not closed on the set of the natural numbers, because 2 - 3 gives a result (-1) which is not a natural number. Division is closed over the rational numbers (the integers {...-2,-1,0,1,2...} plus all the fractions) but division is not closed over the rational numbers, because division by zero doesn't yield any result at all.
You'll notice that mathematics seeks closure by simply inventing numbers that fit; and we will see in the next section why this is legitimate in mathematics. But it doesn't follow from the fact that mathematics can do this that it is legitimate to do this in logic, if logic is supposed to either reflect or apply to the way we reason--and if it doesn't, it's mathematics, not logic. Note, however, that mathematics uses logic (in the ordinary sense), and so presupposes it and is not the same as it. That's one difficulty in trying to make a "mathematical logic." You are taking something that is a particular example of a logical system and trying to use it as a model for the system it is only one particular example of. It wouldn't be surprising if a mathematical logic would work in some cases (those in which the reasoning was similar to what is done in mathematics), but not in others (those cases of logical reasoning that are not in mathematics).
But the real problem in taking mathematics as a model is trying to make logic complete, so that every logical operation on something that is true or false results in something that is true or false. Propositions themselves can be true or false and nothing else; but conclusions can be true, false, or problematic, because inference deals with the necessary truth or falseness of the conclusion based on the truth or falseness of the premises and the type of reasoning involved. Hence, logic as we actually reason necessarily will be incomplete, because, while the conclusion as a proposition has to be either true or false, you can't generate one or the other always from the truth or falsity of the premises.
And if you try to make it complete by simply filling in the truth tables à la mathematics, arbitrarily declaring as "True" certain things which should have question marks, then you get something which does not have an application outside itself, and which (as in the case with the definite and indefinite propositions) has some glaring inconsistencies within itself.
It was a noble effort, but it was doomed to failure, because to model logic on mathematics is a classic case of "reasoning from the particular to the universal," (or from the indefinite to the definite). Of course, there are a lot of contemporary logicians who aren't going to swallow this, because they have Ph. D.s in the field of logic, and have studied it for years and years, and can perform operations using symbolic logic that would make your head spin. And it looks so mathematical! And as everybody since Descartes knows, mathematics is the source of all knowledge and truth.
But let's face it. Contemporary logic is to logic what astrology is to astronomy. You can spend dozens of years studying astrology and can draw charts and all that sort of thing by a very complicated and intricate system that is very difficult to learn; but when all is said and done, astrology rests on the foundation that the earth is at rest in the center of the universe and that the spheres of heaven moving around it cause all the changes on it--and this happens to be false.(8)
By the same token, no matter how complex modern symbolic logic may be, it depends on a radically false epistemology (which is no less strong because it wants to avoid epistemology and thinks you can--which is an epistemological stance in itself) plus the false notion that logic can be modeled after mathematics.
The fact that contemporary logic works well so often is simply a reflection of the fact that mathematical reasoning is a very large subset of logical reasoning; and it isn't surprising that those with a mathematical turn of mind (and who but a person with a mathematical turn of mind would attempt to get into the field of contemporary logic?) would not notice the cases where the applications of their logic were absurd. Hence, they would have no reason to suspect the unsoundness of the logical system itself.
So much for my attack on contemporary logic. I have shown (a) that it doesn't work as applied to statements, (b) why it doesn't work, (c) why it was developed, and (d) why those who are in the field would think that it was a good theory.
To return, then, to the implication as we actually use it, here are the rules:
Rules for the hypothetical syllogism
Inferential mode
1. If the compound and the antecedent are affirmed it follows that the consequent must be affirmed. This valid process is called modus ponens.
2. If the compound is affirmed and the antecedent is denied nothing follows with respect to the consequent.
3. If the compound is affirmed and the consequent is affirmed, nothing follows with respect to the antecedent.
4. If the compound is affirmed and the consequent is denied, it follows that the antecedent must be denied. This valid process is called modus tollens.
Refutational mode
5. If the antecedent and the consequent are affirmed, nothing follows with respect to the compound.
6. If the antecedent is affirmed and the consequent is denied, it follows that the compound is false. This refutes the implication.
7. If the antecedent is denied, nothing follows with respect to the compound.
This is more complex than the other forms of compounding propositions, because here the order in which the two components are placed is significant. Hence, in the inferential mode of reasoning, the first two rules deal with proceeding from the antecedent to the consequent; and the only valid one is modus ponens (the "putting mode" which could be translated as the "affirmational mode," since it goes from affirmation to affirmation). The second two go backwards from the consequent, and in this case, the valid one is the modus tollens (the "taking mode" or "denial mode") of a denial's implying a denial.(9)
The invalid mode "arguing" from the truth of the consequent to the truth of the antecedent is the reason why no scientific theory can be verified. Every scientific theory is of the form "p implies q," because it is giving the cause of the effect in question; and obviously all the theory's predictions are the result of reasoning from the truth of the theory to the necessary truth of the results predicted (modus ponens). But by observing that these predictions are in fact true, when you test the theory, you are now in the mode of reasoning from the consequent to the antecedent, and arguing from the truth of the consequent is invalid. You can refute a theory by showing that its predictions are false, but you can't verify one by its predictions.
And of course, this is why I called arguing from the components to the compound the "refutational" mode of reasoning, because if you analyze what you are doing, you are supposing that the compound's relation to the components in it is an implication (the inferential, normal mode), and you are arguing backwards--in which case, the only valid reasoning is the modus tollens. Contemporary logic has surreptitiously assumed that the components can "generate" the compound as well as the compound "generating" the components, precisely because the refutational mode of reasoning works; but what they didn't see is that the form of the relation of the compound to the components is in all cases "compound implies something about components," not "compound if and only if something about components" (p implies q and q implies p).(10)
Now then, if you want to use contemporary logic as a guide for making inferences, and you want your conclusions to express facts if your premises do, then you have to add to the truth table a column indicating whether the connective is "true" or not: that is, whether it is applicable to these propositions. Just as the truth of the propositions is verified extra-logically, so whether the connective belongs is also verified extra-logically. But once this is done, symbolic logic will follow the rules I have given above.
For those who are interested, here are a couple of examples of what the truth tables will look like:
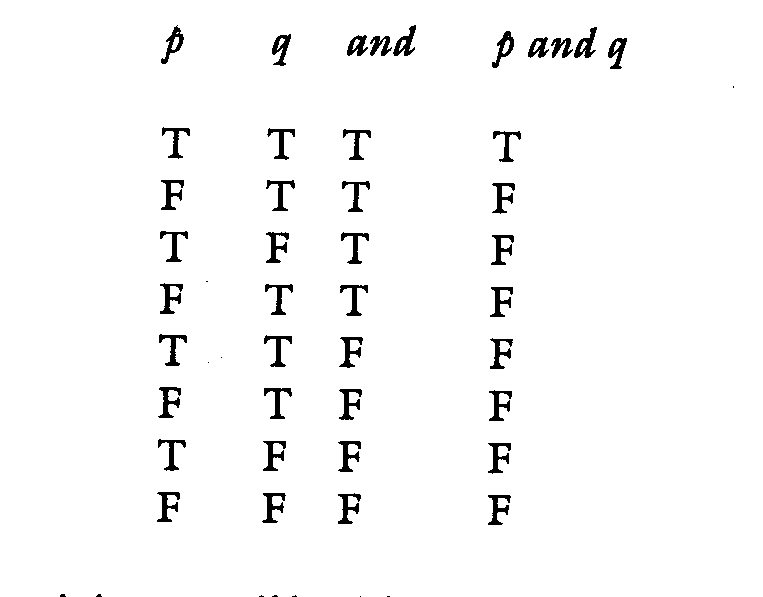

I think you can see what happens. The compound proposition now is false on the last four lines of the table, which is to say whenever the connective is inappropriate. Since contemporary logic ignores these last four lines, it makes the compound true in all these cases, when in fact it isn't.
The truth table for "implies," however, is somewhat peculi can't depend on something false, because there's nothing to depend on if that's the case. Hence, the connective is inappropriate whenever "p" is false, as well as inappropriate sometimes when "p" is true. Therefore, the truth table needs only six lines to cover all the possibilities and make symbolic logic conform to formal implication.
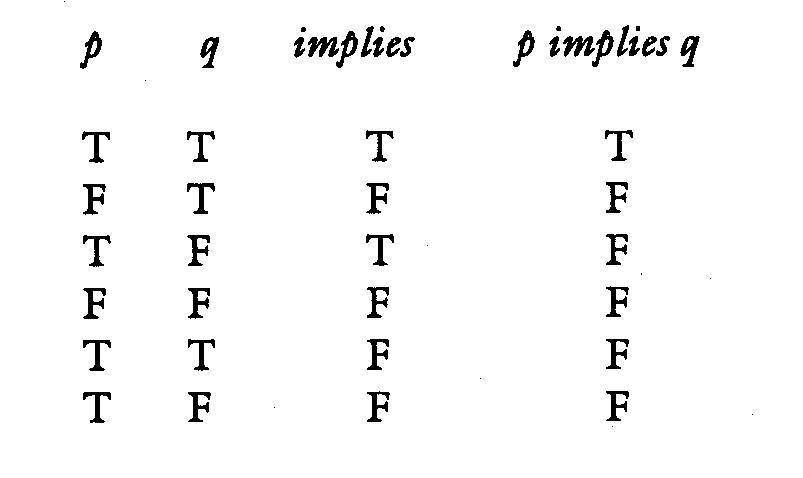
Now of course, since truth tables are not used except at the most elementary level, all of the logical transformations (the "short cuts" and theorems) would have to be worked out taking this extra information into account. But that is not the point of this chapter, and I rather suspect it's not something for me to do. I simply propose it as a suggestion if anyone wants to do logic that looks like contemporary logic, and still guarantee that his conclusions will have to state facts if his premises state facts.
In any case, these are the basic ways of combining propositions. Other connectives we use are more or less complicated combinations of them.
There is one, however, that is quite interesting, because it seems so simple and yet is so complex: "but." I am not talking of "but" as it is usually used in traditional logic (All men are mortal but John is a man, therefore), because that "but" is simply "and" in disguise and is not used that way in ordinary speech.(11)
I am talking about "but" in the sense of "The sun is shining but it is raining."
What does "but" mean? It means, "The statement I am about to utter would seem to be the opposite of what would follow from what I just said and what I just said is true and the statement to follow is true" (which of course implies that the inference you were going to draw from what I just said is invalid). For instance, "The sun is shining, but it's raining" means, "The sun is shining and you might infer that it wouldn't be raining; and (despite that), it's raining." Or, "The sun is shining and you might infer that it's raining, and the inference is not valid, because it's raining."
Schematically, "but" means the following: "p and not-q and not (p implies q)"'--using the symbols from now on to reflect statement logic, not contemporary logic. The thing that keeps it from being a simple "and" connecting an affirmative and negative proposition is the implicit implication that is refuted by it. You wouldn't connect two statements with a "but" unless you expected your hearer to disagree with the second one because of what he thought followed from the first one. So "but" is a way of steering the hearer away from an invalid inference, and preventing him from leaping to a false conclusion. But it isn't treated logically as a separate connective (he said, connecting this statement with the preceding by "but") because (he said giving the antecedent to this consequent) it can be described as a combination of simpler connectives.
I don't suppose it is amiss also to mention "because" as a connective. This gives the conclusion of an inference first, and then the fact that implies it; so the form is "q and (p implies q) and p." So, "I am home because I am not at work" says, "I am home, and if I am not at work, then I am home; and I am not at work." This actually gives what is dependent first and then what it depends on, which reflects the way we reason when we go from effect to cause, and so is more natural actually than showing the relation of dependence (the compound), and then arguing from the independent in that relation to what depends on it--not that this is illegitimate, nor that it might not be clearer in revealing the reasoning process.
Notes
1. I owe this insight to a suggestion from my son.
2. I should point out that some logical notations of the truth table list the column under "p" as I did (TFTF) while others list it (TTFF) and use the former for "q." For practical reasons, I happen to think that the way I did it is preferable, because if there is to be an "r," then the eight lines under the "p" is (TFTFTFTF), that under the "q," (TTFFTTFF), and under the "r," (TTTTFFFF). If there is also to be an "s," then the sixteen lines of these three will just repeat, and you have (TTTTTTTTFFFFFFFF) for "s," and so on. It just makes things easier to write, which, believe me, can be a blessing if you have to go on to "t," "u," and beyond.
3. By the way, conjoining propositions is called "logical multiplication" in contemporary logic, while "and/or" is called "logical addition." Now that you've heard the terms, forget them. This profusion of technical words is to me another way of making the smoke screen contemporary logic is hiding behind thicker.
4. Of course, if I wanted to talk à la contemporary logic, I could get picky and say, "If two statements don't happen simultaneously to be true then they're in fact incompatible with each other (because one is true and the other is false or both are false). But what I'm going to try to establish is that this "factual" sense of incompatibility is never intended by "not both p and q" as a statement.
5. Interestingly, the statement about general statements above is a "is incompatible with" statement, which, if it is couched in the present tense precisely asserts the incompatibility of a statement's being non-tautological with its having predictive force. (And it's obvious from the context that Hume meant this.) But of course incompatibility would allow you to make predictions from it (which the context shows Hume also intended)--which would make it a non-tautological general statement with predictive force. I've never been able to figure out how Hume has been able to get away with some of the things he's said.
6. Of course, here we would run into the informal fallacy of irrelevance, because "q" is in the conclusion and not in the premises. But the inference is formally valid in contemporary logic in any case, and we can permit this in order to eliminate clutter.
7. For some reason, logicians don't seem to like the idea of applying propositional logic to predicate logic. I have made statements about how, based on what I have been saying, statements with subjects and predicates go together (as in the Square of Opposition) below, and have been met with, "Now don't go confusing propositional and predicate logic." For heaven's sake! Don't the propositions in propositional logic have subjects and predicates? In that case, everything that is said in propositional logic will have to be true in predicate logic; though the converse is, of course, not true.
8. Note, by the way, the fact that this is the foundation of astrology means that the science as a science depends on it ("If the earth is at the center, etc., then there is a science of the influences of heavenly bodies on our lives.)--and so by contemporary logic, the fact that this foundation is false implies that the science is a true science. That dilemma in the philosophy of science was pointed out by Carl Hempel.
9. If you want the traditional names for the invalid modes, they are ponendo tollens and tollendo ponens. Even if you don't know Latin, I assume that you're clever enough to figure out what they mean and therefore which they apply to.
10. Note once again that in symbolic logic, the "if and only if" proposition is not the same as "and" because it is true both when both components are true and both are false. Hence, you can "prove" that John is at home if and only if no one else is at home by finding an instance of nobody's being at home. To put it another way, nobody's being at home implies that John is always alone when he's at home.
In actual logic, "if and only if" differs from "and" in that "and" simply asserts some connection in which both have to be true, while "if and only if" means that there is interdependence between the facts indicated by the statements.
11. In fact, it's a translation of the Greek word de, which simply means, "what follows adds to what preceded," rather than alla, the adversative "but," which is our only use of the word "but." We use "and" for additional information as well as for information that is just in general connected with what preceded.
Next